LE PROJET PANA
Notre Destin, SidTrav, Voyageur, etc.


Les stations L4 et les vaisseaux possèdent la même structure. La différence réside dans leurs dimensions et leur vitesse de rotation.
La partie interne est composée d’un cylindre central non tournant de « petit » diamètre et d’un cylindre « creux » tournant qui contient la partie habitée. Le concept est basé sur des idées développées par Arthur C. Clarke d’une part (roman publié en 1973: « Rendez-vous with Rama » ) et Gerard K. O’Neill d’autre part (livre publié en 1976: « The high frontier : Human colonies in Space » ). C’est ce dernier qui a donné son nom aux cylindres tournants (cylindres de O’Neill) pour abriter des habitats dans l’espace. Il s’agit d’utiliser l’accélération centripète du corps tournant pour donner la sensation de gravité.
La différence par rapport au cylindre de O’Neill tel qu’utilisé dans beaucoup de romans de science-fiction est l’utilisation d’un cylindre « creux », faisant apparaître un ersatz de ciel, et réduisant également le volume dédié à l’espace vital à maintenir à la bonne pression avec l’air nécessaire.
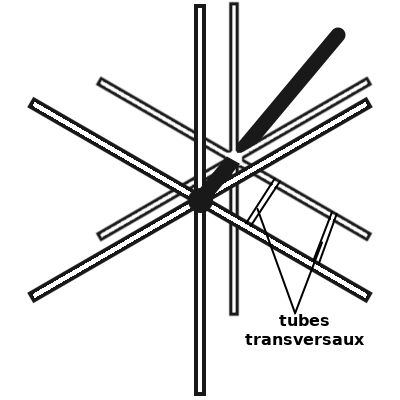
Ce cylindre creux est soutenu et mis en mouvement par un ensemble de dix roues d’entraînement constituées de six rayons, qui sont à la fois des structures de maintien et des moyens de communication. Ces roues sont mises en rotation par des dispositifs dépendant d’un cylindre central non tournant. Ce cylindre est connecté aux autres cylindres non tournants extérieurs, de protection, par ses extrémités. Chaque rayon est relié à son homologue de la roue suivante par deux tubes transversaux parallèles au cylindre central et répartis de manière équilibrée.
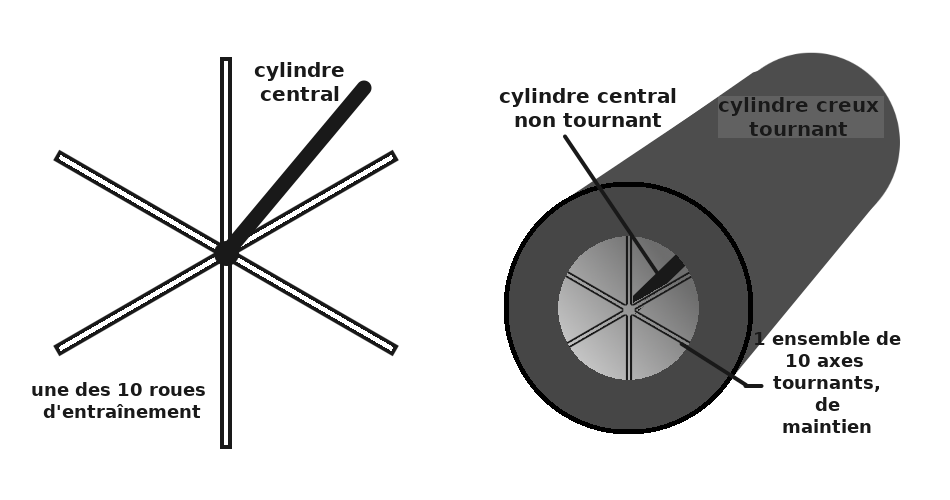
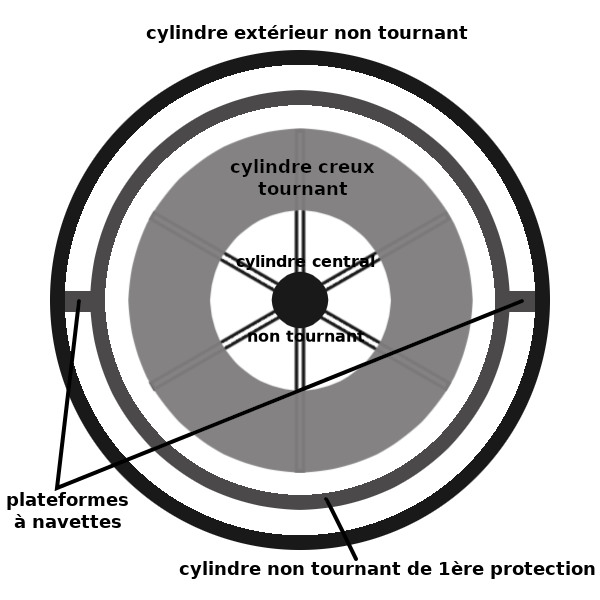
Le cylindre creux tournant de l’habitat est entouré par un cylindre non tournant de première protection. Deux plateformes latérales sont attachées à ce cylindre, pour l’arrivée et le départ des navettes. Le tout est encore protégé par un dernier cylindre non tournant. Tous les éléments non tournants sont connectés par leurs extrémités.
Coupe transversale
Le cylindre creux tournant contient plusieurs sections séparées dont la zone habitée est la plus grande, comme illustré ci-dessous dans la coupe longitudinale.
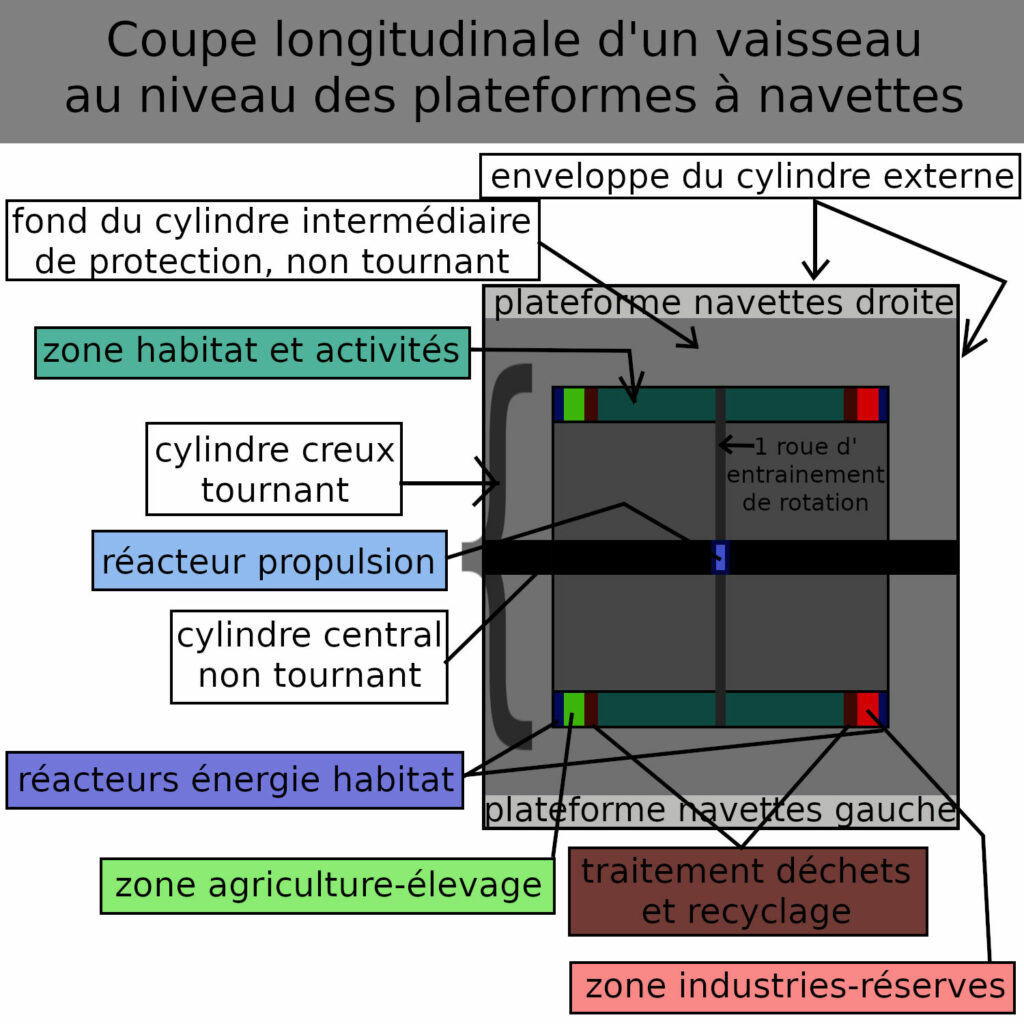
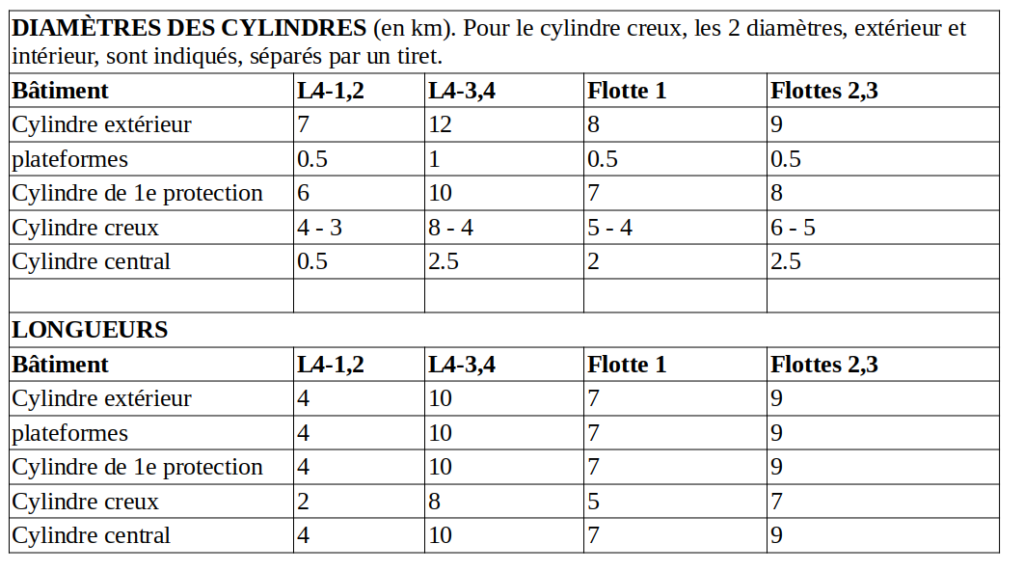
Les dimensions sont présentées dans le tableau ci-dessous.
Pour atteindre une accélération centripète de la même valeur que l’accélération de gravitation sur Terre, la vitesse angulaire de rotation dépend de la dimension du cylindre tournant. Les valeurs sont reprises ci-dessous.
Stations L4-1,2 : 0.67 tour/min
Stations L4-3,4 : 0.47 tour/min
Vaisseaux flotte 1 : 0.597 tour/min
Vaisseaux flottes 2,3 : 0.545 tour/min (voir Tome 2, Voyage vers Pana).
Dans un référentiel tournant, comme le cylindre creux évoqué, il apparaît une pseudo force invoquée pour expliquer la déviation de trajectoire d’un corps observée dans ce référentiel tournant, alors qu’observée depuis un référentiel galiléen, la trajectoire ne dévie pas car aucune « vraie » force ne s’exerce sur le corps. Cette pseudo force est appelée force de Coriolis, et elle est donc liée à la rotation du référentiel. Pour avoir une idée de l’importance de cette force, on la compare aux autres forces en action. Ou plutôt, on va comparer les accélérations associées. Dans le cas du cylindre tournant, on considère l’accélération centripète, générant l’effet gravitationnel, et l’accélération de Coriolis. Cette dernière dépend de la vitesse de rotation du référentiel tournant (le cylindre creux), de la vitesse du corps en mouvement dans ce référentiel et de la direction de son déplacement. Elle est nulle si la vitesse est parallèle à l’axe de rotation du cylindre et maximale si la vitesse est perpendiculaire à cet axe, c’est-à-dire soit vers le « haut » soit le long d’une courbe de section perpendiculaire à l’axe.
Dans le cas des stations ou vaisseaux concernés, les vitesses angulaires sont de l’ordre de 0.5 tour/min ; l’accélération de Coriolis dépend donc seulement de la vitesse du corps. Un coureur sportif faisant du 10km/h (2.78 m/s), dans une direction perpendiculaire à l’axe de rotation, subit une accélération de Coriolis de 0.29 m/s**2, c’est-à-dire 3 % de l’accélération gravitationnelle, ce qui est loin d’être négligeable. Mais s’il court parallèlement à l’axe, il n’y aura pas d’effet. Toutes les grandes infrastructures sportives sont orientées le long de l’axe de rotation et cette direction est renseignée partout. Cet axe est défini comme l’axe « Nord-Sud », le Nord étant la partie avant du bâtiment. De cette façon, l’ouest et l’est sont référencés comme sur Terre par rapport au nord et au sud.
Pour des explications illustrées de qualité supérieure, je vous conseille deux excellentes vidéos Youtube de la chaîne « Les idées froides » (https://www.youtube.com/@Lesideesfroides):
https://www.youtube.com/watch?v=FlpHs8Oy1fo
https://www.youtube.com/watch?v=qtoTU8C8LG8
Les vaisseaux d’une même flotte voyagent quasi en parallèle, à la même vitesse, et sont séparés par une distance suffisamment grande pour que, à la vitesse qu’ils auront acquise (6000 km/s), ils aient suffisamment de temps pour réagir en cas de mise en danger des autres vaisseaux. Le temps choisi est de plus ou moins une heure, et la distance entre les vaisseaux fixée à 28 millions de kms.
Les habitants des vaisseaux ont la possibilité de se rendre sur les autres, grâce à des navettes. Elles doivent acquérir suffisamment de vitesse pour parcourir les 28 millions de kms en un temps raisonnable, sans toutefois soumettre les voyageurs à une accélération trop grande. La vitesse maximale atteinte est de 333 km/s, en un jour. De cette façon, l’accélération maximale subie est de plus ou moins une fois l’équivalent de l’accélération gravitationnelle sur Terre, dénotée par le symbole 1g.
Le voyage entre deux vaisseaux adjacents est alors de 2 jours.
